NÚMEROS RACIONALES
OPERACIONES
SUMA Y RESTA DE FRACCIONES
La suma (o resta) de dos o más números
racionales de distinto denominador es la suma (o resta) de racionales
equivalentes a los dados, obtenidos por el procedimiento de común denominador.
Pasos a seguir:
1º
Se selecciona un común denominador, es decir un múltiplo común (si es posible
el menor múltiplo que exista) a los denominadores de las fracciones sumandos.
2º
Se divide el común denominador por cada denominador de las fracciones sumandos
y se multiplica el resultado por el numerador respectivo.
3º
Se suman (o restan, según los signos de las fracciones sumandos) los
numeradores obtenidos.
4º
Se simplifica la fracción obtenida, si fuera posible.
Por
ejemplo:
Para tener en cuenta: Para los
números racionales se cumplen las mismas condiciones que para los números
enteros, es decir, si dos racionales son de igual signo, se suman y el resultado
posee ese signo; mientras que si son de distinto signo, se restan y el
resultado lleva el signo del racional de mayor valor absoluto.
¿Cómo resolver ejercicios que incluyan más de una suma y/o resta?
Para sumar y/o restar varios números racionales se
puede proceder de distintas maneras:
Ejercicios
1) Resolver estas sumas de fracciones
(simplificar cuando sea posible):
2) Hallar las siguientes diferencias
(simplificar cuando sea posible):
3) Calcular:
4) Encontrar con las soluciones el
camino que debe seguir el caballo blanco para llegar hasta el tablero de ajedrez:
5) Plantear y resolver.
a) Silvia echa en una jarra 3/4 litro de jugo de fruta y 1/2 litro de leche. ¿Qué fracción de líquido echa en la jarra?
b) Jaime tiene una botella de batido de 3/4 litro. Echa en una taza 1/5 litro. ¿Qué cantidad queda en la botella?
c) Gasté 1/5 y luego 2/3 de una suma de dinero. ¿Qué parte gasté y qué parte me queda?
d) Para comprar un juego yo aporté 1/3 del total del precio, mi hermana 1/9 y mi papá el resto. ¿Qué parte del
costo del juego aportó mi papá?
e) Una persona recorre 2/5 de una montaña en una primera etapa y en una segunda etapa 1/3 del total. ¿Qué fracción del total constituye la etapa que le falta por recorrer?
MULTIPLICACIÓN Y DIVISIÓN DE FRACCIONES
Multiplicación
El producto de dos o más números racionales expresados como fracción es otra fracción que tiene por numerador el producto de los numeradores y por
denominador el producto de los denominadores de las fracciones dadas y cuyo
signo se obtiene aplicando la regla de los signos.
Ejemplos:
División
El
cociente de dos números racionales expresados como fracción es otra fracción que se obtiene multiplicando
el dividendo por el inverso del divisor y cuyo signo se obtiene aplicando la
regla de los signos.
Ejemplos:
Para tener en cuenta: Para los números
racionales se cumplen las mismas condiciones que para los números enteros, es
decir, si se multiplican o dividen dos racionales de igual signo, el
resultado es positivo; mientras que si son de distinto signo, el
resultado lleva el signo negativo.
¿Cómo resolver ejercicios combinados?
Para resolver ejercicios combinados con
fracciones se deben seguir algunas reglas y tener en cuenta el mismo orden de
jerarquía de las operaciones que hemos aprendido tiempo atrás al trabajar con
ejercicios combinados con números enteros. También, se debe tener presente que,
cuando es posible, se deben simplificar los resultados de las operaciones que
se van resolviendo.
Ejemplos:
Problemas
Ejemplo: Un campo mide 2000 metros cuadrados
Ejemplos:
1) Obtener los siguientes productos:
2) Efectuar las siguientes divisiones:
a)
¿Cuántos bombones se comieron cada una?
b)
¿Qué fracción de bombones se comieron entre las dos?
5)
En el juego de ajedrez al inicio de la partida, y mientras se mantengan todos
en juego, los peones ocupan 1/4 del tablero. ¿Cuántas
casillas representa esto?
6)
Los 2/5 de las 50 personas que
viajan en un avión son niños. ¿Cuántos adultos viajan en el avión?
7)
Un coche lleva circulando 26 minutos, en los cuales ha recorrido 2/3 de su trayecto.
¿Cuánto tiempo empleará en recorrer todo el trayecto, yendo siempre a la misma
velocidad?
8)
He estado 2 días de excursión. El primer día me gasté 1/2 del dinero que tenía y
el segundo, 2/5 de lo que me quedaba.
Si tenía 80 euros, indicar cuánto dinero me ha sobrado.
a)
40 euros b) 20 euros
c) 24 euros d) 2 euros
9) Un obrero que debe abrir una zanja de 65 m . de largo ha hecho
primero los 2/13 de la misma y luego el
doble de lo ya hecho. ¿Qué longitud debe abrir aún?
POTENCIACIÓN Y RADICACIÓN DE FRACCIONES
La potenciación y la radicación son las
únicas operaciones cuyos procedimientos de resolución son iguales tanto para
bases y radicandos enteros como para bases y radicandos racionales. Por lo
tanto para resolverlas se deben seguir los mismos métodos que hemos aprendido
tiempo atrás al trabajar con números enteros.
Potenciación
La
potencia n (donde n es un número natural, y se lee enésima) de un número
racional se obtiene al multiplicar n veces dicho número racional.
Ejemplos:
Para tener en cuenta: La potenciación
de números racionales también se puede resolver aplicando la propiedad
distributiva de la potenciación de números enteros respecto a la división. Por
lo tanto, es lo mismo, por ejemplo:
Radicación
La
raíz n (donde n es un número natural mayor o igual a 2, y se lee enésima) de un
número racional es otro número racional tal que este último elevado al exponente
n sea igual al primer número racional.
Ejemplos:
Para tener en cuenta: La radicación
de números racionales también se puede resolver aplicando la propiedad distributiva
de la radicación de números enteros respecto a la división. Por lo tanto, es lo
mismo, por ejemplo:
Además,
para los números racionales se cumplen las mismas condiciones que para los
números enteros, es decir, que a radicando positivo e índice par
corresponden dos soluciones, mientras que a radicando negativo e índice
par no hay solución.
Propiedades de la potenciación
Entre las propiedades que cumple la
potenciación de números racionales, nos centraremos en las que hemos estudiado
anteriormente para los números enteros; pero además, en el último inciso,
haremos hincapié en una nueva propiedad:
à
Producto de potencias de igual base: el
producto de potencias de igual base es otra potencia de la misma base que las
potencias dadas y cuyo exponente es la suma de los exponentes dados. Ejemplo:
à
Cociente de potencias de igual base: el cociente
de potencias de igual base es otra potencia de la misma base que las potencias
dadas y cuyo exponente es la resta de los exponentes dados. Ejemplo:
à
Potencia de otra potencia: la
potencia de otra potencia es otra potencia de la misma base cuyo exponente es
el producto de los exponentes dados. Ejemplo:
à El cero como exponente:
todo número racional, distinto de cero, elevado a la potencia cero es 1.
Ejemplo:
à Potencia
con exponente entero negativo: toda potencia de un número
con exponente entero negativo es igual al inverso de dicho número con exponente
opuesto (o sea, positivo). Ejemplo:
Propiedades de la radicación
La
radicación de números racionales cumple las mismas propiedades que ya hemos
estudiado para los números enteros:
à
Propiedad recíproca distributiva de la raíz
respecto a la multiplicación: el producto de raíces de
igual índice, es otra raíz del mismo índice, cuyo radicando es el producto de
los radicandos de las raíces dadas. Ejemplo:
à Propiedad recíproca distributiva de la raíz respecto a la
división: el cociente de raíces de igual índice, es otra
raíz del mismo índice, cuyo radicando es el radicando del dividendo dividido el
radicando del divisor. Ejemplo:
à
Raíz de otra raíz: es otra
raíz con el mismo radicando, cuyo índice es el producto de los índices dados.
Ejemplo:
¿Cómo resolver ejercicios combinados?
Los ejercicios combinados con fracciones se
resuelven siguiendo el orden de jerarquía que ya hemos estudiado al ver
ejercicios combinados con números enteros. Además, como hemos mencionado
anteriormente, cuando es posible, se debe simplificar (convenientemente
mientras se va resolviendo).
Ejemplo:
Ejercicios
1) Calcular
las siguientes potencias.
2)
Hallar las siguientes raíces:
5) Efectuar las operaciones siguientes:
6)
Colocar un paréntesis para obtener el resultado.
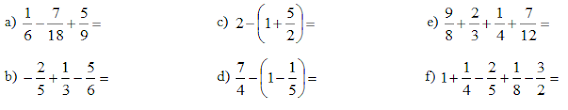
No hay comentarios.:
Publicar un comentario