Números Racionales

NÚMEROS RACIONALES

INTRODUCCIÓN   

    Al trabajar con las operaciones con números enteros, se vio la imposibilidad de resolver una división en la cual el resto sea distinto de cero, en otras palabras, que el dividendo no sea múltiplo del divisor; así, por ejemplo, dada la operación -9:2, no existe ningún número entero que sea el resultado de la misma.

   Para poder resolver esta clase de divisiones, se crearon los llamados números racionales, que pueden ser representados de distintas maneras, las más conocidas son las fracciones y los decimales.

   Los números racionales expresados como fracciones

   Se llama fracción al cociente indicado de dos números enteros a y b (distinto de cero).

   Una fracción se representa a/b, donde a se llama numerador y b denominador.

  El conjunto formado por todas las fracciones se llama conjunto de los números racionales y se simboliza con Q (inicial de la palabra anglosajona quotient, que significa cociente).

   Algo de historia

   En la antigüedad los hombres se dieron cuenta que no todo se podía medir con los que hoy conocemos como números naturales, sino que a veces era necesario considerar una parte de un todo, y de estas situaciones surgieron los números racionales.

  Los más antiguos documentos que se conocen donde se encuentran números racionales, es la piedra roseta y los papiros de Rhind y de Moscú, ambos de la cultura egipcia, que datan de hace unos 4000 años. En ellos se puede apreciar el conocimiento que tenían los egipcios de las fracciones positivas, en particular de las fracciones unitarias (aquellas con denominador 1), las cuales se representaban por dos símbolos: el numerador con un óvalo y el denominador (abajo o al lado) con el símbolo asociado al número correspondiente. Y a cualquier otra fracción no unitaria, los egipcios la escribían como suma de fracciones unitarias distintas.

   También otras civilizaciones conocían las fracciones: los babilónicos utilizaban aquellas cuyo denominador era una potencia de 60, mientras que los griegos y romanos manejaban también las fracciones unitarias, cuyo uso persistió hasta la época medieval.

  En el siglo XIII, Leonardo de Pisa (también conocido como Fibonacci) introdujo en Europa la barra horizontal para separar numerador y denominador en las fracciones.

  A principios del siglo XV, el árabe Al Kashi fue el que generalizó otra forma de representar a los números racionales que no sea utilizando fracciones: surgían así los números decimales, los cuales recién en el siglo XVII comenzaron a escribirse separando con un punto o una coma la parte entera de la parte decimal.

   El nombre de número racional proviene de ración, o sea, parte de un todo.

   ¿Dónde se utilizan los números racionales expresados como fracciones?

  Las fracciones se aplican para expresar la razón entre dos cantidades, la parte de un todo y para expresar porcentajes. En la vida real, por ejemplo, un uso muy común es para expresar la cantidad de un alimento o bebida; en áreas del conocimiento como la contabilidad se puede mencionar que las empresas utilizan las fracciones para expresar el dinero que manejan haciendo una relación entre el dinero que entra y el que sale, las ganancias y las pérdidas; en la física un uso es para relacionar la distancia recorrida en función del tiempo gastado en recorrerla. 

   Ejercicios 

   Después de esta introducción, les proponemos las siguientes actividades iniciales (de repaso) que podrán resolver a partir de los conocimientos adquiridos en la escuela primaria.

1) Es el cumpleaños de Gregorio y su mamá le preparó una torta para compartir con sus 19 compañeros de clase durante la fiesta que le organizó en casa.

a) Dibujar la torta y dividirla de modo que todos los chicos puedan comer la misma cantidad.

b) Pintar la porción que le corresponde a Gregorio.

c) ¿Cómo pueden expresar con una operación la parte que le toca de torta a Gregorio?

d) ¿Cómo pueden expresar con un número la parte que le toca de torta a Gregorio? ¿De qué tipo de número se trata?

2) Escribir la fracción representada:

a)                                                                    b)

                                           

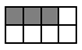
3) Marcar con una cruz la fracción que corresponde a la figura

a) 4/9                b) 5/9                c) 4/5                d) 5/4

4) Representar gráficamente la fracción 

a) 2/3                 b) 5/9               c) 13/7

5) a) ¿Qué parte de un mes de 30 días representan 3 días?

b) ¿Qué fracción del tablero de ajedrez representan las casillas blancas?

6) Esteban está de cumpleaños e invitó a 5 amigos. Dividió la torta para que él y sus amigos coman la misma cantidad. Los primeros en llegar fueron Javier y Camila; Esteban le sirvió una porción a cada uno. Representar gráficamente las porciones que les dio a sus primeros invitados. ¿Qué fracción de la torta les dio? ¿Qué fracción de la torta quedó?

7) Investigar si los números enteros son o no números racionales. ¿Por qué?

   FRACCIONES EQUIVALENTES

   Las fracciones que ocupan la misma parte del entero se llaman equivalentes y representan el mismo número racional. Para obtener fracciones equivalentes, multiplicamos o dividimos el numerador y el denominador por un mismo número.

   Simplificar fracciones

   Cuando el numerador y el denominador se dividen por el mismo número, decimos que simplificamos la fracción. La fracción que no puede simplificarse se llama irreducible.

                                   

   Ejercicios

1) Don Jaime tiene una pizzería. Un día vinieron 4 chicas y pidieron una pizza para compartir.

a) Dibujar la pizza y dividirla de modo que todas las chicas puedan comer la misma cantidad.

b) Pintar la parte que le toca a una de las chicas.

c) ¿Cómo pueden expresar con una operación la parte de pizza que le toca a cada chica?

d) ¿Cómo pueden expresar con un número la parte de pizza que le toca a cada chica?

2) ¿Cuáles de las fracciones encontradas en los ejercicios dados en las actividades anteriores (ver guía de ejercitación más arriba) se pueden simplificar? Escribir la fracción irreducible para las mismas.

3) Determinar cuáles de estas fracciones son equivalentes a 6/8.

4) Para las siguientes fracciones encontrar otra fracción que sea equivalente a la dada.

5) Transformar las fracciones siguientes en otras equivalentes cuyo denominador sea el indicado en cada caso.

6) Encontrar las fracciones irreducibles para:

7) ¿Qué parte del total del cubo son los cubitos sombreados? Hallar la fracción irreducible.

8) Encontrar la fracción equivalente a 4/7 tal que la suma de su numerador con su denominador sea igual a 99.

   REPRESENTACIÓN EN LA RECTA NUMÉRICA

   Para representar fracciones en la recta numérica se divide cada unidad en tantas partes iguales como indica el denominador y se toman tantas partes como indica el numerador.

   Ejemplos:

   Para tener en cuenta:

·   Siempre se parte desde la primera unidad, es decir del cero al uno, si la fracción es positiva, ó del cero al uno negativo, si la fracción es negativa.

·   Cuando el numerador es mayor que el denominador, en el cual las partes de la primera unidad no alcanzan para tomar las que indica dicho numerador; se debe continuar dividiendo en igual partes la siguiente unidad en la recta y así sucesivamente hasta obtener el número de partes que se deben tomar.

   Ejercicios 

1) Representar en la recta numérica las siguientes fracciones:

2) Escribir la fracción que representa el punto en cada recta numérica y justificar tu respuesta.

3) Indicar qué número representa en la recta numérica el punto señalado.

4) Hallar una fracción equivalente a 8/6 y representarla en la recta numérica. ¿A ambas fracciones les corresponde el mismo lugar?

   ORDEN

   Para comparar dos fracciones existen muchos procedimientos: utilizar la representación gráfica (si son positivas), hallar dos fracciones equivalentes con igual denominador, ubicarlas en la recta numérica, pasarlas a su representación decimal, entre otros.

   Un procedimiento fácil para comparar dos fracciones es el siguiente:              

   Para tener en cuenta: Al igual que para los números enteros, se cumple que si tenemos dos números racionales, uno positivo y uno negativo, siempre es mayor el racional positivo.

   Ejercicios 

1) Colocar correctamente el signo de desigualdad (< ó >) entre cada uno de los pares de números siguientes:

2) En las últimas vacaciones, los Méndez gastaron 7/8 de sus ahorros; y los García, 5/6. Si tenían ahorrada la misma cantidad de dinero, ¿cuál de las familias gastó más?

3) Durante una partida de ajedrez los peones de un bando, que son las piezas de menor importancia, pueden llegar a recorrer 7/8 del tablero; mientras que un alfil, una pieza de mayor rango, puede llegar a moverse por 1/2 del tablero. ¿Cuál de estas piezas pueden llegar a andar por mayor parte del tablero? 

4) A los 3 minutos de haber comenzado una carrera de bicicletas, Andrés había recorrido 4/15 del circuito, Joaquín 3/10 y Leandro 2/13. ¿Quién iba ganando hasta el momento?

5) En una competencia deportiva, Vanina completó la vuelta en 15/8 de minuto, Vanesa en 17/9 de minuto y Verónica en 19/10 de minuto. ¿Quién ganó la carrera?              

6) Ordenar de menor a mayor.