SISTEMAS DE ECUACIONES
(De 2 ecuaciones con 2 incógnitas)
INTRODUCCIÓN

Existen problemas de la vida
diaria donde es necesario encontrar más de una incógnita. Y usar el “método del
tanteo” puede ser tedioso o, hasta incluso, inútil. Para resolverlos de forma
sencilla y segura resulta conveniente plantear sistemas de ecuaciones.
Los sistemas de ecuaciones son un conjunto de dos o más ecuaciones con varias incógnitas que conforman un
problema matemático que consiste en encontrar los valores de las incógnitas que
satisfacen todas las ecuaciones.
Ejemplos:
Aclaración: El símbolo { al principio representa que el sistema de ecuaciones
abarca el conjunto de todas ellas.
Nosotros nos centraremos en el
trabajo de sistemas de dos ecuaciones
lineales o de primer grado
(porque las variables sólo aparecen elevadas a la primera potencia) con dos incógnitas (representadas por las letras x e y).
Sistemas de dos ecuaciones con dos incógnitas
Se llama sistema de dos ecuaciones de primer grado con dos incógnitas, a
todo par de ecuaciones con dos incógnitas que tengan solución común, es decir, la misma solución.
Ejemplos:
Clasificación de los sistemas de ecuaciones
Según la cantidad de soluciones que posean, los sistemas de ecuaciones se
clasifican en:
à
Sistema
compatible determinado.
à
Sistema
compatible indeterminado.à Sistema incompatible.
Hay distintos métodos para resolver sistemas de ecuaciones; entre los que existen nosotros estudiaremos:
à Método de igualación.
à Método de sustitución.
à Método gráfico.
MÉTODO DE IGUALACIÓN
El Método de Igualación para
resolver sistemas de ecuaciones consiste en igualar (de ahí su nombre)
expresiones obtenidas al despejar la misma incógnita de ambas ecuaciones, para
luego resolver una única ecuación con una incógnita.
Para aplicar este método se deben seguir los siguientes pasos:
Para aplicar este método se deben seguir los siguientes pasos:
1. Se
despeja de ambas ecuaciones una de las incógnitas (la misma).
2. Se
igualan las expresiones obtenidas en el paso anterior y se resuelve la ecuación
armada para hallar el valor de una de las incógnitas.
3. Se
sustituye el valor de la incógnita hallado en el paso 2 en, al menos una, de
las ecuaciones del paso 1, para obtener el valor de la otra incógnita.
4. Se
verifica el resultado hallado (opcional).
Ejemplo:
Ejemplo:
1. En este
caso despejaremos la incógnita y,
aunque, al finalizar la resolución, se obtendrá el mismo resultado que si
despejamos x.
1°
ecuación: 2x + 3y = 7 2°
ecuación: -3x + 4y = -2
3y = 7 - 2x 4y = -2 + 3x
y = (7 - 2x):3 y = (-2 + 3x):4
2. Como ambas expresiones anteriores son iguales a y, también son iguales entre sí, por lo que podemos igualarlas.
2. Como ambas expresiones anteriores son iguales a y, también son iguales entre sí, por lo que podemos igualarlas.
(7 - 2x):3 = (-2 + 3x):4
4.(7 - 2x) = 3.(-2 + 3x)
4.(7 - 2x) = 3.(-2 + 3x)
28 - 8x
= -6 + 9x
28 + 6 = 9x
+ 8x
34 = 17x
34:17 = x
2 = x
3. Sabiendo
ya que x = 2, reemplazamos en las
ecuaciones originales.
y =
(7 – 2x):3 y = (-2 + 3x):4
y = (7 – 4):3 y = (-2 + 6):4
y
= (7 – 4):3 y
= (-2 + 6):4
y = 3:3 y
= 4:4
y = 1 y
= 1
Hemos obtenido que la solución del sistema
es x = 2 e y = 1, que puede expresarse (2; 1) también.
Como el sistema tiene una única solución es
un sistema compatible determinado.
4.
Verificamos 2x + 3y = 7 -3x + 4y
= -2
2.2 + 3.1 = 7 -3.2 + 4.1 = -2
4 + 3 = 7 -6 + 4 = -2
7 =
7
-2 = -2
A veces sucede que algunos sistemas de
ecuaciones poseen más de una solución y éstas siguen un cierto patrón.
Ejemplo:
Ejemplo:
1. 1°
ecuación: 2x + y = 8 2°
ecuación: 10x + 5y = 40
y = 8 - 2x 5y = 40 - 10x
y = (40 - 10x):5
8 - 2x
= (40 - 10x):5
5.(8 - 2x) = 40 - 10x
40 - 10x = 40 - 10x
40 - 40 = 10x - 10x
0 = 0x
0 = 0
Hemos llegado a una igualdad donde la
incógnita ha desaparecido. Lo mismo hubiera ocurrido si despejamos x.
Como 0 siempre será igual a 0, la ecuación
tiene infinitas soluciones y el sistema es compatible indeterminado.
Algunas soluciones son:
(-1;
10) 1° ecuación: 2.(-1) + 10 = 8 2° ecuación: 10.(-1) + 5.10 = 40
-2 + 10 = 8 -10 + 50 = 40
8
= 8
40 = 40
(0;
8) 1° ecuación: 2.0 + 8 = 8 2° ecuación: 10.0 + 5.8 = 40
0 + 8 = 8
0 + 40 = 40
8 = 8
40 = 40
(1;
6) 1° ecuación: 2.1 + 6 = 8 2° ecuación: 10.1 + 5.6 = 40
2 + 6 = 8
10 + 30 = 40
8 = 8
40 = 40
Las infinitas soluciones de este sistema
comparten el siguiente patrón: cuando x
aumenta en una unidad, y disminuye en
dos unidades.
Un sistema sin solución
En ocasiones podemos
encontrarnos con sistemas de ecuaciones que no tienen solución, es decir, no
existe ningún valor de x y de y que sea solución de ambas ecuaciones
al mismo tiempo.
Ejemplo:
1. 1°
ecuación: x + y = 8 2°
ecuación: 4x + 4y = 40
y = 8 - x
4y = 40 - 4x
y = (40 - 4x):4
2.
8 - x
= (40 - 4x):4
4.(8 - x) = 40 - 4x
32 - 4x = 40 - 4x
-4x + 4x = 40 - 32
0x = 8
0 = 8
Hemos llegado a una igualdad donde la
incógnita ha desaparecido. Lo mismo hubiera ocurrido si despejamos x.
Pero esta igualdad nunca es cierta, pues 0
no es igual a 8 (0 ≠ 8). Por lo tanto, la ecuación no tiene solución y el
sistema es incompatible.
Ejercicios
1)
Resolver cada uno de los siguientes sistemas.
2)
Determinar si cada uno de los sistemas dados es compatible determinado,
compatible indeterminado o incompatible.
3)
Escribir un sistema de dos ecuaciones cuya solución sea:
a)
x = 1, y = 2 b) x
= 3, y = 1 c) x
= 2, y = 3
MÉTODO DE SUSTITUCIÓN
El Método de Sustitución para
encontrar la solución de sistemas de ecuaciones consiste en sustituir (por eso
el nombre del método) la expresión obtenida de una de las ecuaciones al despejar
alguna de las incógnitas en la otra ecuación por su valor correspondiente.
Para utilizar este método se deben seguir
los siguientes pasos:
1. Se
despeja de alguna de las ecuaciones una de las incógnitas.
2. Se
sustituye la expresión obtenida en el paso anterior en la otra ecuación y se
resuelve la ecuación armada para hallar el valor de una de las incógnitas.
3. Se
reemplaza el valor de la incógnita hallado en el paso 2 en la ecuación del paso
1, para obtener el valor de la otra incógnita.
4. Se
verifica el resultado hallado (opcional).
Ejemplo:
1. En este
caso elegiremos despejar la incógnita y
de la primera ecuación, aunque, al finalizar la resolución, se obtendrá el
mismo resultado que si despejamos x o
si comenzamos trabajando con la segunda ecuación.
1°
ecuación: 2x + 3y = 7
3y = 7 - 2x
y = (7 - 2x):3
2. Como la expresión
anterior es igual a y, podemos sustituir
la misma en el valor correspondiente de la otra ecuación.
-3x
+ 4y = -2
-3x + 4.[(7 - 2x):3] = -2
-3x + [(28 - 8x):3] = -2
(28 - 8x):3 = -2 + 3x
28
- 8x = 3.(-2 + 3x)
28 - 8x = -6 + 9x
28 + 6 = 9x
+ 8x
34 = 17x
34:17 = x
2 = x
3. Sabiendo
ya que x = 2, reemplazamos en la
ecuación que elegimos al principio.
y = (7 – 2x):3
y = (7 – 2.2):3
y = (7 – 4):3
y = 3:3
y = 1
Hemos obtenido que la solución del sistema
es x = 2 e y = 1, que puede expresarse (2; 1) también.
Como el sistema tiene una única solución es
un sistema compatible determinado.
4.
Verificamos 2x + 3y = 7 -3x + 4y
= -2
2.2 + 3.1 = 7 -3.2 + 4.1 = -2
4 + 3 = 7 -6 + 4 =
-2
7 =
7
-2 = -2
Ejercicios
1) Resolver
los siguientes sistemas de ecuaciones por el método de sustitución.
2) Determinar si cada
uno de los sistemas dados es compatible determinado, compatible indeterminado o
incompatible.
MÉTODO GRÁFICO
Para usar este método se deben seguir los
siguientes pasos:
1. Se
despeja de la incógnita y de ambas
ecuaciones.
2. Se
representan gráficamente en los ejes cartesianos ambas rectas asociadas a las
ecuaciones del sistema (una forma conveniente es utilizar la pendiente y la
ordenada al origen).
3. Se
observa cuál es el punto de intersección de ambas rectas. Las coordenadas de
dicho punto son la solución del sistema de ecuaciones.
4. Se
verifica el resultado hallado (opcional).
Ejemplo:
Ejemplo:
1. Despejamos
la incógnita y para cada ecuación.
1°
ecuación: 2x + 3y = 7 2°
ecuación: -3x + 4y = -2
3y = 7 - 2x
4y = -2 + 3x
y = (7 - 2x):3 y = (-2 + 3x):4
y = 7/3 - 2/3 x y = -2/4 + 3/4 x
y = 2,3 - 2/3 x y = -0,5 + 3/4 x
2.
Reconocemos pendiente y ordenada al origen de cada ecuación despejada
anteriormente y con ellas graficamos las rectas correspondientes.
1° recta: y = 2,3 - 2/3 x 2° recta: y = -0,5 + 3/4x
Pendiente: -2/3 Pendiente: 3/4
Ordenada:
2,3 Ordenada:
-0,5
3. Para
determinar la solución del sistema observamos si existe un punto de
intersección entre las rectas graficadas.
Hemos llegado visualmente a que la solución
del sistema es x = 2 e y = 1, que puede escribirse también como
las coordenadas del punto (2; 1).
Este sistema tiene una única solución, por
lo tanto es un sistema compatible determinado.
4.
Verificamos 2x + 3y = 7 -3x + 4y
= -2
2.2 + 3.1 = 7 -3.2 + 4.1 = -2
4 + 3 = 7 -6 + 4 =
-2
7 =
7
-2 = -2
3) Micaela
está tratando de encontrar el número de soluciones posibles para un sistema de
dos ecuaciones lineales. Ella dibuja la siguiente gráfica, la cual muestra
parte de las dos rectas del sistema. ¿Qué puede concluir?
a)
El sistema no tiene solución.
b)
El sistema tiene una solución.
c)
El sistema tiene dos soluciones.
d)
El sistema tiene soluciones infinitas.
PROBLEMAS
Los sistemas de ecuaciones se
consideran una herramienta muy útil para resolver problemas. En muchas
situaciones cotidianas, así como en problemas relacionados con otras
disciplinas, se presenta la necesidad de averiguar dos o más incógnitas
vinculadas entre sí por distintas relaciones que pueden expresarse mediante
ecuaciones.
Entre las áreas del
conocimiento que utilizan los sistemas de ecuaciones se puede mencionar a la economía,
donde se usa para establecer el punto de equilibrio en los mercados entre la
oferta y la demanda; la física, en donde se emplea para hallar en qué momento y
a qué distancia se encontrarán dos móviles que se desplazan a una cierta
velocidad; la química, que aplica los sistemas de ecuaciones para el balanceo
de reacciones.
Una aplicación a la vida
diaria puede ser el problema presentado al principio de esta página:
-Nosotros compramos tres gaseosas
y tres hamburguesas. En total gastamos $21.
-Yo
comí dos hamburguesas y me tomé una gaseosa. Pagué $12.
-¿Cuánto costará cada hamburguesa? ¿Y cada gaseosa?
A partir de la pregunta planteada se
puede establecer que las incógnitas de este problema son el precio de cada hamburguesa
(x) y el precio de cada gaseosa (y).
Luego, desde la información
vinculada a cada incógnita se puede deducir que el sistema de ecuaciones
buscado es
Por último, utilizando cualquiera de los
métodos de resolución estudiados se puede concluir que la solución es x = 5 e y = 2, es decir, cada hamburguesa cuesta $5 y cada gaseosa $2.
Ejercicios
1) La maestra Stricter dejó como tarea
de matemática los siguientes desafíos numéricos:
a) Hallar dos números cuya suma es 28
y su diferencia es 12.
b) Hallar dos números sabiendo que si
uno de ellos se suma con el doble del otro se obtiene 21, y que si este último
se suma con el doble del primero resulta 18.
c) La suma de dos números es 150, y el mayor excede
en 4 al menor. ¿Cuáles son los números?
2)
3) A principio de año la señora Doris
de la escuela primaria de Springfield realizó una venta de
artículos escolares para recaudar fondos para mejoras en la cafetería. Vendió 30 artículos
entre mochilas y cuadernos y recaudó $813. ¿Cuántos artículos vendió de cada
uno si el precio era de $80 para las mochilas y $11 para los cuadernos?
4) Lisa está muy preocupada por su
futuro y decide averiguar cuánto le costarán sus estudios universitarios. En la
universidad de Yale la colegiatura más la pensión cuestan $8400 mensuales. La
pensión cuesta $600 más que la mitad de la colegiatura. ¿Cuánto cuesta la
colegiatura y cuánto la pensión?
5) Cletus debe averiguar el número de
animales de su granja, pero sólo sabe que la suma de patos y vacas es 132 y la
de sus patas es 402. ¿Cuántos patos y cuántas vacas tiene?
6) Luego de 17
partidos sin perder, el equipo de fútbol infantil de la primaria de Springfield
ha reunido 27 puntos. ¿Cuántas veces ganó y cuántas empató?
7) El señor Burns compró un terreno rectangular
adjunto al de su planta nuclear. El mismo tiene un perímetro de 392 metros . Calcular sus
dimensiones sabiendo que mide 52
metros más de largo que de ancho.
8) a) Hace 4 años la edad del jefe Górgory
era nueve veces la edad de su hijo Rafa, y dentro de 8 años será el triple.
¿Cuáles son sus edades actuales?
b) Dentro de 5 años Luann,
la mamá de Milhouse, tendrá el triple de la edad de su hijo. Hace 6 años, la
suma de sus edades era 38. ¿Cuántos años tiene cada uno?








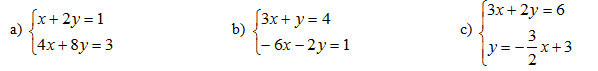










No hay comentarios.:
Publicar un comentario