NÚMEROS REALES
INTRODUCCIÓN
Conjunto numérico
Se llama conjunto numérico a una agrupación de números que
comparten una serie de características y propiedades. Por
ejemplo: el conjunto de los números Naturales, el conjunto de los números Enteros, el conjunto de los números Racionales, entre otros.
Subconjunto numérico
Se dice que un conjunto numérico es subconjunto de otro conjunto
numérico cuando todos sus números pertenecen también al otro
conjunto. Por ejemplo: el conjunto de los números pares es un subconjunto
del conjunto de los números Naturales.
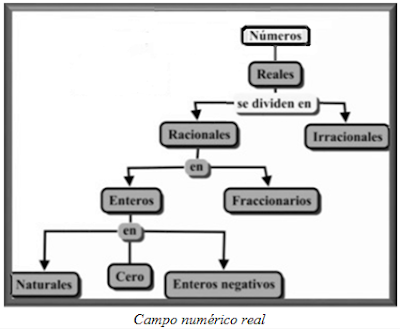
NÚMEROS REALES
El conjunto de los números Reales está formado por dos clases de números: los Racionales y los Irracionales. Todos ellos están comprendidos entre “menos
infinito” y “más infinito” y se corresponden uno a uno con alguno de todos los
puntos que integran la recta real. Este conjunto se simboliza con la letra R.
Conjunto de los números Racionales
El conjunto de los números Racionales está integrado por
todos los números que se pueden escribir como fracción; su expresión decimal
es exacta o es periódica. Informalmente se lo define como el
conjunto que sirve “para medir”. Este conjunto se representa con la letra Q.
Conjunto de los números Enteros: dentro del conjunto de los números
racionales, aquellos números cuales su expresión decimal es exacta y no
lleva coma se llaman números enteros. El conjunto de los números Enteros es un subconjunto de los números Racionales. Este subconjunto se
simboliza con la letra Z.
Conjunto de los números Naturales: a su vez, dentro
del conjunto de los números Enteros, a los números que son positivos se
les denomina números naturales. Comúnmente se lo conoce como el conjunto
que sirve “para contar”. El conjunto de los números Naturales es un subconjunto
de los números Enteros. Este subconjunto se representa con la letra N.
Conjunto de los números Irracionales
El conjunto de los números Irracionales está compuesto por todos
los números que no pueden ser expresados como fracción; su expresión decimal
tiene infinitas cifras decimales no periódicas. Este conjunto se
simboliza con la letra I, aunque
también puede denotarse Q* -en
particular si trabajamos más allá del conjunto de los números reales.
Los tres números irracionales más famosos, y que tienen nombre propio,
son: Pi (π = 3,14159…); el número Áureo o de Oro (φ = 1,61803…); y el número de
Euler o constante de Napier (e =
2,71828…). Estos números, en apariencia “raros” y “difíciles” para
operar, son de gran relevancia tanto en Matemática como en otras disciplinas,
así como también en nuestro entorno diario.
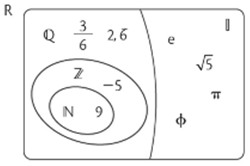
Diagrama de Venn que muestra la relación entre los conjuntos numéricos
Ejercicios
1) Clasificar cada
número como miembro de uno o más de los siguientes conjuntos: racionales,
irracionales y/o reales.
a) -3/4 b) -3,14152161718... c) √7
2) Clasificar los siguientes
números, según corresponda, en: número real, número irracional, número
racional, número entero, número natural o ninguno de las anteriores.
a) -5 b) 3/5 c) 3π d) 2 e) -1/4 f) 6,3
g) 0 h) √5 i) √-1 j) 0,3782 k) √4 l) -18/7
3) Mencionar 5 números reales
(2 irracionales y 3 racionales) que se encuentren en los siguientes intervalos.
a) (-9; 26) b) [12; ∞) c) (-√4; 3] d) (-0,2; -0,0003) e) (-π; π)
NÚMEROS IRRACIONALES
Radicales
Dentro del
conjunto de los números irracionales existen números que se denominan
radicales. ¿Qué los caracteriza? Son expresiones de la forma ⁿ√a (donde el
índice n es un número natural mayor o igual a 2 y el radicando a es un número
real, con la condición de que cuando a es negativo n ha de ser impar) que no representan
números racionales.
Por ejemplo √2 es un radical pues no puede
simplificarse para hallar la raíz cuadrada y √2 = 1,4142135…; pero √4 no lo es,
pues √4 = 2 que es un número racional.
Ejercicios
1) Determinar cuáles de las
siguientes raíces son radicales.
2) Escribir un radical que
cumpla las condiciones dadas:
a) Índice par y radicando
entero.
b) Índice múltiplo de 3 y
radicando fraccionario.
c) Índice impar y radicando
negativo.
No hay comentarios.:
Publicar un comentario